Programming basics

Welcome!
The main thing you need to know before you start programming is what a program really is.

In general one sentence – a computer program is a set of written instructions that are generally executed sequentially when the program is running. Generally when you start a program you actually make the computer execute it.
All the instructions that the computer is making are essentially storing, copying, calculating and comparing values that are stored in its’ memory.
A set of instructions and conditions that can be executed in order to achieve a certain result is called an algorithm.

Input and Output

Any meaningful program will usually perform a task that require some input, make calculations and decisions according the the given input and generate output according to the instructions written in the program.

Any information that is given to the program is called input.
Any information that the program exposes to any external element is called output. An external element might be a computer screed, a printer, files, or some other program.

Defining first!

The first thing you have to do when you want to write a program is to define the required input for the program, define the desired output that is generated by the program, and define the logical steps that are required in order to convert the input given to the program to the desired output.
In many cases the input and the output of the program are not well defined at first, or you might have some assumptions regarding the input and output, so before you start to write the program you have to make sure that all the required input, desired output, and the actual logic is well defined.

For example – when we want to execute the task of counting to 10, we have a well defined input that the counting stops at 10, but without any other information about the task we naively assume that the counting starts at 1, and incremented by steps of 1, resulting in the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10.
In this example we don’t have any defined output – do we need to write the numbers, or do we need to count them out loud? The answer to this question depends on the context of the task. Usually, when we ask a person to count to a specific number we want to him to say the numbers out load, or by heart and have a specific pause between each number. But when we talk about a computer program, the easiest way to show that we count is by displaying the numbers on the screen.

So you can see that when we need to define a very easy and intuitive task we find that there are some parameters that are not originally defined in the task, and we have to define them before we start to do the actual programming. After well defining the task we end up with the following more detailed definition: Count from 1 to 10 at steps of 1 and print each number on the screen. (In this task description we still have vague definitions like “print on the screen” – there can be several ways to print the numbers on the screen – we will address this issue in the future).

Variables

Variables are places in which we store information that is needed in order to perform the task. In most cases the variables we will use will have a meaningful name that will describe the information stored in them and their purpose. In our example we have 4 variables that we use in order to store 4 different values:

1. The starting point of our count – We will call it “Start”.
2. The ending point of our count – We will call it “End”.
3. The increment step we use in our count – We will call it “Step”.
4. The current number we reach during our counting – We will call it “Counter”.

We use the variables’ names in our logic when we want to describe an operation that involves them.

Program logic

After we defined our program’s input, output and logic, we need to break down the logic we defined to small steps that will be performed in our program. Defining the required steps will result in an algorithm that can be used in order to perform the task. An algorithm is a sequence of operations and rules that define how the input is handled and transformed to the required output. One way to express an algorithm is by using a flowchart.

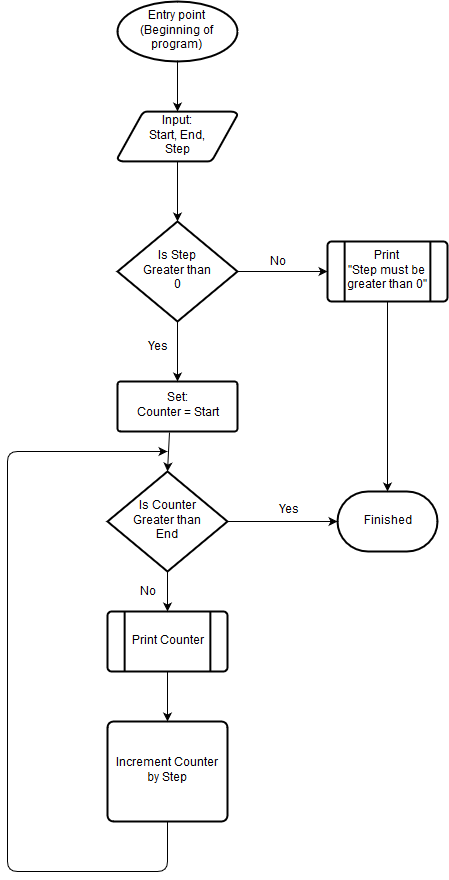
An algorithm for counting from a specific initial number (We will call it “Start”) to a specific final number (We will call it “End”) in specific steps (We will call it “Step”) can be described by the following flowchart:

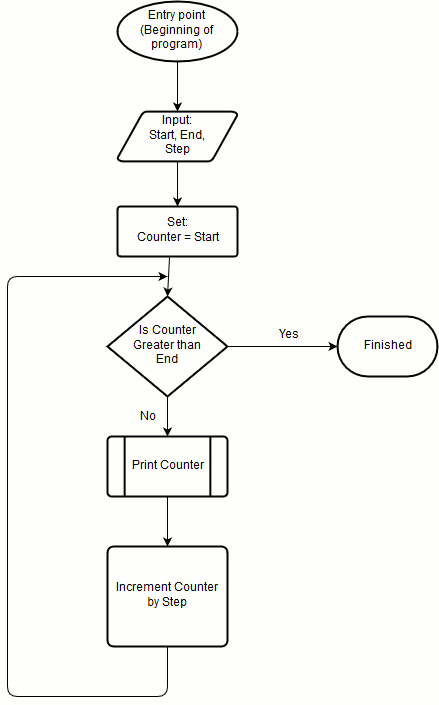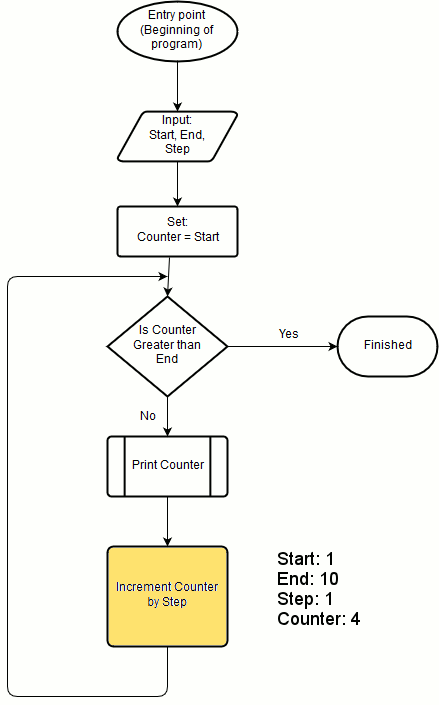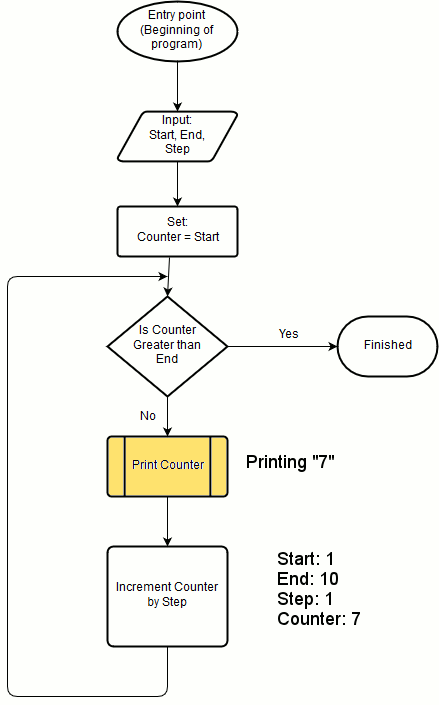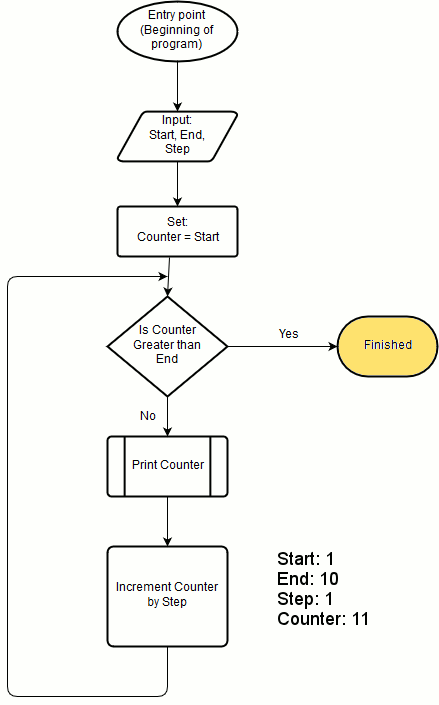
Understanding the flowchart

In order to understand the flowchart you need to go through the different steps according to the arrows directions.

1. The initial step of the flowchart is the Entry point.
2. Following the arrow from the entry point we reach the Input step, in which we can request the input from the user, or use predefined values.
3. After the input step we reach a condition step, in which, we check if our Counter is greater then our End number.
4. If it is – we follow the arrow labeled “Yes” and we reach the end of the program.
5. If it is not – we follow the arrow labeled as “No” and reach the following step, which is the “Print” step.
6. In the print step we will print the current counter to the screen using a predefined functionality that is available to us in the framework we are using.
7. The next step is the Increment step in which we increment our counter by the value of “Step” we previously defined.
8. After the “Increment” step  we have an arrow that is merged back to the position of just before the condition, meaning that we now go to step 3 above, and we need to check again our counter value against the value of the “End” number we previously defined.

So according to this chart we will continue incrementing our counter until it is greater than our Ending number – so our ending number will also be printed to the screen. The program will finish when the condition on step 3 will make us to reach step 4. Note that we can reach steps 3, 5, 6, 7 and 8 multiple times, but because we change our counter in step 7, each time we go through these steps the value of counter will be different, resulting in a potentially different behavior each time. Especially in steps 3, which will make a different decision according to the counter’s value, and step 6 which will result in printing different values according to the actual value of our counter.

Assumptions and Bugs

Sometimes, when you define your task’s algorithm, you make certain assumptions whether you realize it or not. Even in this small example we might assume that the value for our “Step” parameter is positive.

Exercise: What will be the program’s output in case the value of the “Step” variable is negative? (Check the answer)

Input validation

Once you realize that you have assumptions regarding your input variables you have to define how you want to address different cases of incompatibility.
The most easy way to address such cases is to verify that the variables have compatible values for your logic, and in case they are not compatible – generate output that will indicate that the input is not compatible with the program’s requirements.
A better way to address such cases is to understand the meaning of such values, and modify the algorithm so it will be able to handle meaningful cases that were not previously defined.

We can use our counting example in order to demonstrate the two cases:

1. In case we don’t see how a non-positive step value for is meaningful – we can add a new condition step that will check if the value in “Step” is less than 1, and if it is – print a message to the screen that say that “the Step value must be greater than 0”.

   

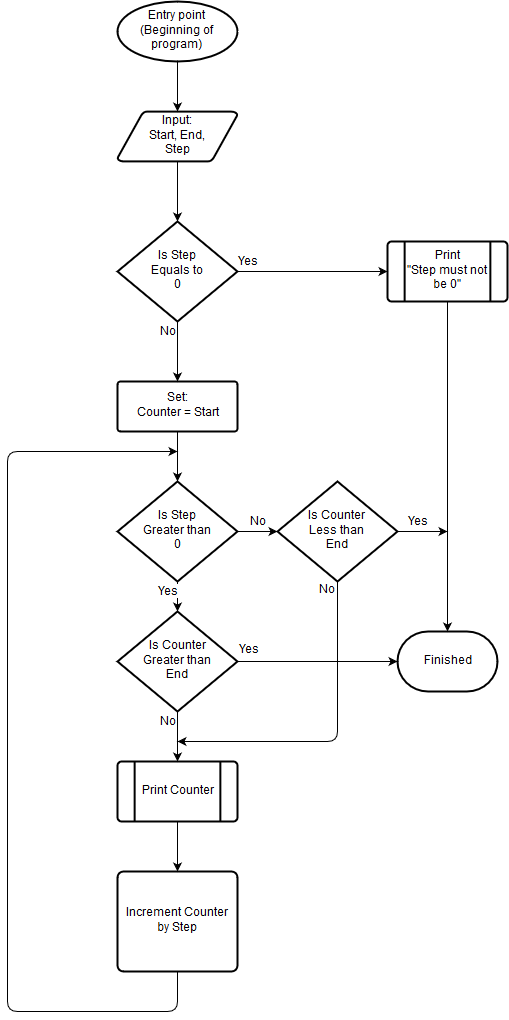
2. We can decide that a negative Step value can be meaningful if we want to count backwards.
   In this case we will also add a condition step that will check if the value of “Step” is positive (larger than 0), and if it is we will execute our original logic.
   But – if the value of “Step” is negative (less than 0) – we will need to perform a little different logic.
   Note that if the “Step” value is 0 – we will probably have to generate an output that says that we can’t count in steps of 0.
   Also note that in both negative and positive Step values – we increment our counter by Step. The result of incrementing by a negative value is decrementing.